Основы теоретической физики/Движение в центральном поле

1.4.4. Движение в центральном поле

Внешнее поле, в котором потенциальная энергия зависит только от расстояния до определенной неподвижной точки, называется «центральным полем».

У центральных полей есть два важных свойства: 1. Сила, действующая на материальную точку в центральном поле, зависит только от радиус-вектора $\overrightarrow{r}$ и направлена вдоль него в каждой точке. Шаблон:ОТФ

2. Траектория движения частицы в центральном поле, лежит в одной плоскости. Это свойство прямо следует из предыдущего. Поскольку движение происходит в одной плоскости, то функцию Лагранжа удобней рассматривать в полярных координатах. Для одной материальной точки: Шаблон:ОТФ

Можно заметить, что в  Шаблон:ОТФ  нет зависимости от обобщенной координаты $\phi$. Всякую обобщенную координату, не входящую в явном виде в функцию Лагранжа, называют «циклической координатой».

Рассмотрим уравнение движения для произвольной циклической координаты $q_c$: Шаблон:ОТФ

То есть из  Шаблон:ОТФ  можно сделать вывод: обобщенный импульс, соответствующий циклической координате – сохраняется.

Для случая движения материальной точки в центральном поле, из уравнения движения для циклической координаты $\phi$, подставляя определение проекции момента импульса  Шаблон:ОТФ  получим: Шаблон:ОТФ

Как видим, проекция момента импульса на ось, совпадающую с направлением центрального поля – сохраняется.

Полученный закон сохранения проекции момента импульса можно продемонстрировать графически. Рассмотрим для этого бесконечно малый отрезок произвольной траектории частицы.

Рис.1.7

Найдем площадь сектора, образованного двумя бесконечно близкими радиус-векторами и элементом дуги траектории: Шаблон:ОТФ

Если поделить обе части выражения  Шаблон:ОТФ  на dt, то получим формулу для «секторальной скорости»: Шаблон:ОТФ

То есть сохранение момента означает и постоянство секторальной скорости: Шаблон:ОТФ

Мы получили закон, который называется «Второй закон Кеплера»: в центральном поле, частица движется так, что за равные промежутки времени, радиус-вектор описывает равные площади.

Рассмотрим теперь полную задачу о движении частицы в центральном поле. Удобнее всего эту задачу решать пользуясь законами сохранения энергии и момента импульса, а также определением проекции момента на ось «z» в цилиндрических координатах  Шаблон:ОТФ : Шаблон:ОТФ

В формуле  Шаблон:ОТФ  энергия, масса и момент импульса – это постоянные величины, значит из  Шаблон:ОТФ  можно выразить скорость: Шаблон:ОТФ

Из скорости теперь можно найти зависимость координаты от времени (траекторию), однако для этого нужно знать точный вид функции U(r). В общем виде, для произвольной потенциальной энергии, можно найти функцию, обратную траектории - зависимость времени от координаты: Шаблон:ОТФ

Также можно найти зависимость угла поворота от времени если воспользоваться соотношением Шаблон:ОТФ : Шаблон:ОТФ

Формулы  Шаблон:ОТФ  и  Шаблон:ОТФ  – это и есть решение задачи движения тела в центральном поле. При этом,  Шаблон:ОТФ  – дает связь $\phi (r)$, то есть является уравнением траектории, а  Шаблон:ОТФ  – определяет расстояние движущейся точки как функцию времени.

Величину $\frac{M_z^2}{2m{r}^2}$ – называют «центробежной энергией». Индекс оси «z» у момента, обычно в формулах не пишут.

По определению, «эффективной потенциальной энергией» называется величина, которая находится из соотношения: Шаблон:ОТФ

Полученные формулы  Шаблон:ОТФ  и  Шаблон:ОТФ  будут иметь физический смысл лишь в том случае, если подкоренное выражение в них больше, либо равно нулю. Поэтому можно определить «границы области движения» как точки траектории, для которых выполняется соотношение: Шаблон:ОТФ

На границах области движения скорость тела равна нулю, эти точки называют еще «точками поворота», поскольку при достижении этих точек, координата тела переходит от увеличения к уменьшению или наоборот.

Легко заметить, что определяющее точки поворота квадратное уравнение  Шаблон:ОТФ  может иметь два корня $r_{min}$ и $r_{max}$. Это радиусы двух окружностей, ограничивающих область движения.

Если область движения имеет только одну границу $r\ge r_{min}$, то такое движение – инфинитно. То есть траектория материальной точки приходит из бесконечности и уходит в бесконечность.

Рис. 1.8

Если область движения имеет две границы $r_{min}\le r\le r_{max}$, то такое движение финитно. Траектория частицы лежит внутри кольца, ограниченного окружностями $r=r_{min}$ и $r=r_{max}$.

Рис. 1.9

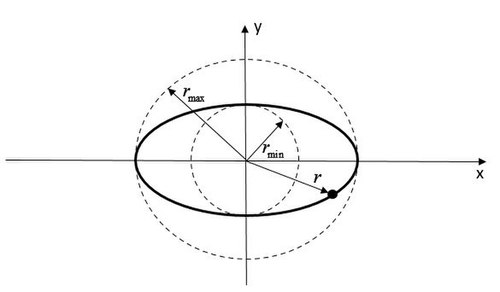
Следует отметить, что траектория финитного движения не обязательно замкнута. Условие, при котором траектория является замкнутой, можно найти из формулы  Шаблон:ОТФ . За время, когда расстояние r до точки меняется от $r=r_{min}$ до $r=r_{max}$ и обратно, угол изменится на величину: Шаблон:ОТФ

С другой стороны, чтобы траектория была замкнутой, необходимо выполнение условия: Шаблон:ОТФ

где m и n – это целые числа. Только если выполняется  Шаблон:ОТФ , через n повторений, радиус-вектор частицы сделает m полных оборотов и совпадет со своим первоначальным значением. То есть условием замкнутости траектории является равенство: Шаблон:ОТФ

Чтобы узнать, выполняется ли равенство  Шаблон:ОТФ , нужно знать точный вид функции U(r). Например, можно доказать, что для функций $U\sim \frac{1}{r}$ и $U\sim \frac{1}{r_2}$, равенство  Шаблон:ОТФ  всегда выполняется, то есть для таких полей, траектории финитных движений всегда замкнуты.

Можно также легко показать, что при движении в центральном поле, частица никогда не сможет попасть точно в центр. Действительно, если учитывать, что подкоренное выражение в  Шаблон:ОТФ  должно быть больше нуля, то получим: Шаблон:ОТФ

То есть «падение» частицы в центр возможно лишь при бесконечной потенциальной энергии.

См. также

<<Назад  |  Далее>>
Оглавление